Javaで順列生成アルゴリズムを実装する - アルゴリズム学習(その1)

アルゴリズムを勉強しようと思って、以下の本のアルゴリズムをJavaで自分で考えて再実装するという取り組みをやっている。以下の本は基本的なアルゴリズムが簡単に説明されていて、しかも薄いのでやりやすい。2011-09-22を見て購入した。

作者:長尾和彦
技術評論社

それで最初に順列生成の話が出てきたので、まずはこれを作ってみた。実装は https://github.com/shibayu36/algorithm-study/tree/master/java-data-structure-and-algorithm においてある。

順列の内容をprintlnする関数を作る

まずは簡単に順列の内容をprintlnする関数を作ってみる。

この本に書いてあった説明がいまいちわからなかったので、順列生成のアルゴリズムを説明しているブログ記事とかを探して実装した。

まず、http://www2.cc.niigata-u.ac.jp/~takeuchi/tbasic/BackGround/Permutation.html によると、樹形図を模倣すれば良いらしく、アルゴリズムは次のようになる。

既に得られた順列に，使える文字をその順列に付け加えて，新たな順列を作ると言うものです。

そして，そのようにして得られた順列に対して，同様な処理を施し，

必要な長さの順列が得られるまで続ける

またサービス終了のお知らせを見ると、なんとなく操作のイメージが湧いたので、引用。

perm 第 1 引数第 2 引数
----------------------------------
│ (1 2 3 4) ()
│ ^
再 ↓
帰 │ (2 3 4) (1)
呼 │ ^
び ↓
出 │ (3 4) (2 1)
し │ ^
↓
│ (4) (3 2 1)
│ ^
↓
() (4 3 2 1) 並べ方完成
図 : 関数 perm の動作（その１）

というわけで、まずは必要な長さの順列を作ったらprintする関数を作ってみた。

import java.util.ArrayList;
import java.util.List;

// とりあえずSystem.out.printlnするやつ
public class Permutation1 {
    public static void make(List<Integer> data) {
        // 候補の配列
        List<Integer> candidate = new ArrayList<>(data);
        // 順列の配列
        List<Integer> perm = new ArrayList<>();
        _make(candidate, perm);
    }

    private static void _make(List<Integer> candidate, List<Integer> perm) {
        if (candidate.size() == 0) {
            // 候補が無くなったらpermに順列が出来ているので
            // println
            System.out.println(perm.toString());
        }

        // candidateの全ての文字を一つずつピックアップして
        for (int i = 0; i < candidate.size(); i++) {
            List<Integer> p = new ArrayList<>(perm);
            List<Integer> c = new ArrayList<>(candidate);
            // permの最後にその文字を追加して
            p.add(c.get(i));
            // 候補からその文字を除外して
            c.remove(i);
            // さらにステップを進める
            _make(c, p);
        }
    }
}

まあなるほどという感じ。

順列の内容をprintlnする関数を作ってみる

上記だと結果が標準出力に入るだけなので、次は結果を返すような関数を作ってみる。

import java.util.ArrayList;
import java.util.List;
public class Permutation2 {
    public static List<List<Integer>> make(List<Integer> data) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> candidate = new ArrayList<>(data);
        List<Integer> perm = new ArrayList<>();
        return _make(result, candidate, perm);
    }

    private static List<List<Integer>> _make(List<List<Integer>> result, List<Integer> candidate, List<Integer> perm) {
        if (candidate.size() == 0) {
            result.add(perm);
        }
        else {
            for (int i = 0; i < candidate.size(); i++) {
                List<Integer> p = new ArrayList<>(perm);
                List<Integer> c = new ArrayList<>(candidate);
                p.add(c.get(i));
                c.remove(i);
                _make(result, c, p);
            }
        }

        return result;
    }
}

やっていることはほぼ同じで、結果を格納するresultという変数も引き回しながら、結果を標準出力にprintしている部分をresultにaddするようにしただけ。

しかし、これを見てみると、あまり綺麗じゃないというイメージを持つ。これを作った時、個人的には以下の二点で違和感を感じた。

resultというmutableな変数を引き回して、それに追加していくのがエレガントではない
再帰呼び出しをしているものの、階乗を出すときのような分かりやすい再帰的な構造にはなっていない
- 階乗はn! = n * (n - 1)!のように、f(n-1)を使ってf(n)を求める分かりやすい式になっている

これらから、もうちょっと調べて改良することにした。

再帰的な構造を利用するアルゴリズムに改良する

順列の生成とList内包表記 - 趣味的にっきによると、アルゴリズムとしては、

与えられたリストから要素を1つ取り出して、残りの要素から再帰的に順列を求めて、それらを結合する

ということらしい。先程よりなんとなくシンプル。

さらに Python で順列を生成 | すぐに忘れる脳みそのためのメモのイメージ図が分かり易いので引用する。

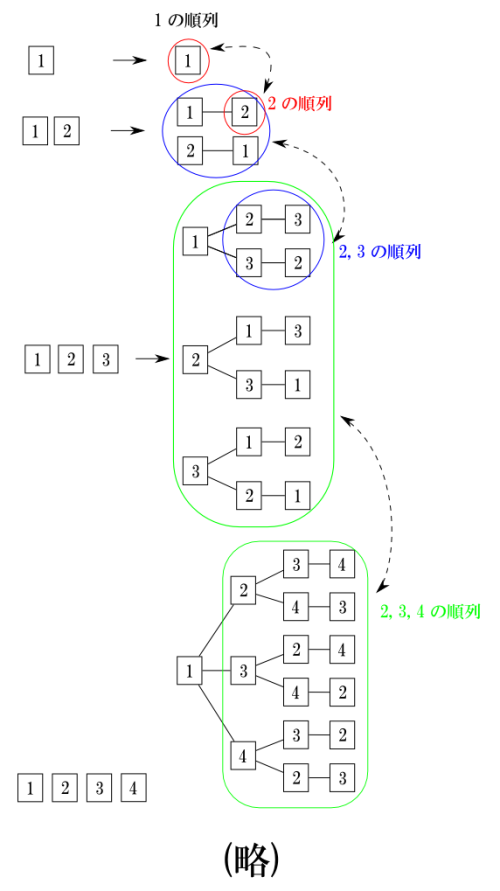
自分の言葉でアルゴリズムを書いてみると、

1. 渡された配列から、1文字(ch)ずつピックアップする
2. chを除いた配列(rest = candidate - ch)を使って再帰呼び出しし、残りの文字の順列のリストを得る
3. restの順列のリストの全ての先頭に、chを結合する
4. 全文字ピックアップして同じ処理をしたら、得られたリストを全て結合する

という感じだろうか。1と4はflatMapとかを使ったらできそう。3はmapを使ったらできそう。2は単なる再帰呼び出しっぽい。

以上でアルゴリズムのイメージは出来たので、実際に実装してみる。

import java.util.ArrayList;
import java.util.List;
import java.util.stream.Collectors;
public class Permutation3 {
    public static List<List<Integer>> make(List<Integer> candidate) {
        // 候補がないなら、順列は空リストを返す
        if (candidate.size() == 0) {
            List<List<Integer>> empty = new ArrayList<>();
            empty.add(new ArrayList<>());
            return empty;
        }

        // candidateから1文字ずつピックアップする
        // flatMapを使ってるので1文字はiに格納されるはず
        return candidate.stream().flatMap(i -> {
            // 残りの配列はcandidateからiを省いたものである
            List<Integer> rest = new ArrayList<>(candidate);
            rest.remove(i);
            // 残りの配列で順列のリストを作り、
            // 先頭にピックアップした文字を結合
            return make(rest).stream().map(list -> {
                list.add(0, i);
                return list;
            });
        }).collect(Collectors.toList());
        // flatMapを使っているので、1文字ずつピックアップして
        // 全文字の操作が終わったら、全ての操作で得られたリストを
        // 結合して返しているはず
    }
}